Modélisation architecturale de forme libre
Galerie d’arts d’Alberta, par Randall Stout Architects
Rhino est connu pour sa capacité unique à travailler avec des géométries NURBS (B-spline rationnelle non uniforme). La géométrie NURBS possèdes des qualités essentielles pour en faire la meilleure option pour la modélisation 3D/CAO.
- Géométrie complexe précise : Les NURBS peuvent représenter de façon extrêmement précise tout type de géométrie : courbes, cercles, ellipses, sphères ou tores, géométrie de forme libre complexe comme les carrosseries de voiture ou les corps humains.
- Fichiers plus légers : la quantité d’informations nécessaire pour générer une géométrie complexe est bien inférieure en utilisant des NURBS qu’avec toute autre méthode.
- Points de contrôle : les courbes et surfaces NURBS sont très intuitives et prévisibles lorsqu’elles sont modifiées avec leurs points de contrôle.
Les objets de VisualARQ sont compatibles avec les NURBS et peuvent être créés à partir d’une géométrie NURBS.
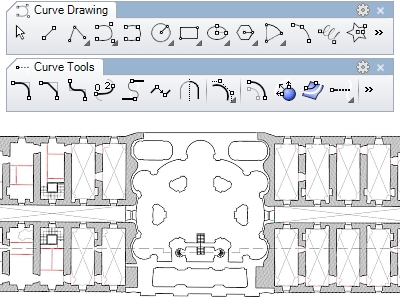
Courbes
- Création de courbes : lignes, polylignes, rectangles, polygones, cercles, ellipses, courbes à partir des points de contrôle, courbes par point interpolés…
- Édition de courbes : congé, chanfrein, décalage, prolonger, limiter, diviser, joindre, reconstruire… Les courbes peuvent être modifiées avec les points de contrôle.
- Des courbes aux objets 3D : Les murs, les murs-rideaux, les poutres, les garde-corps, les portes, les fenêtres, les ouvertures, les dalles et les toits de VisualARQ peuvent être créés à partir de courbes. Les surfaces et les solides peuvent également être créés à partir de courbes.
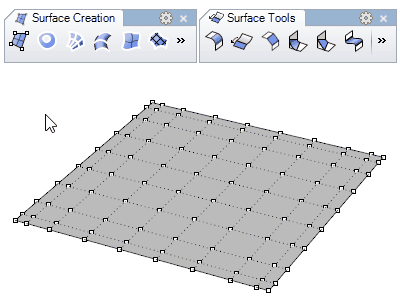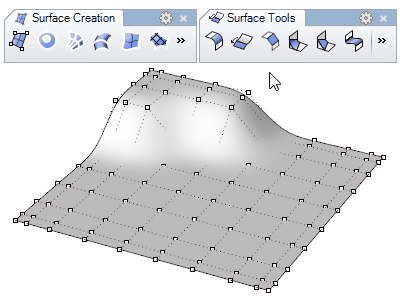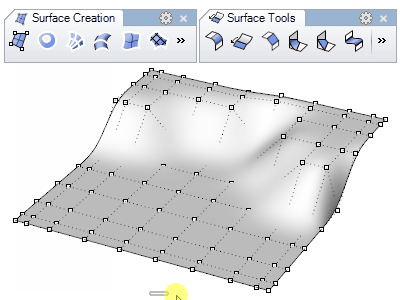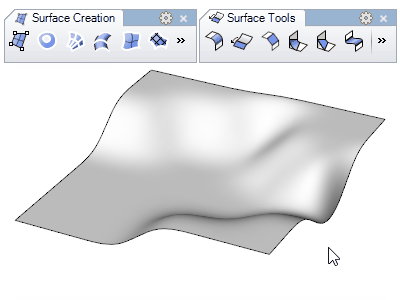
Surfaces
- Création de surfaces : à partir de points, courbes, bords de solides, surfaces par sections, révolutions, balayages, patchs…
- Modélisation de surfaces : congé, chanfrein, décalage, prolonger, limiter, diviser, joindre, reconstruire… Les surfaces peuvent être éditées en déplaçant leurs points de contrôle.
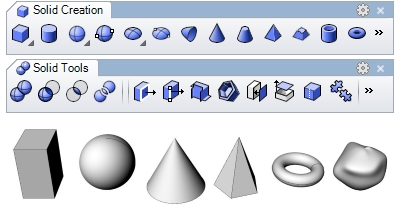
Solides
- Formes primitives : boîte, cylindre, sphère, ellipsoïde, cône, pyramide, tube, tore…
- Modélisation de solides complexes : opérations booléennes, déplacer des bords, des faces, évider, ajouter des trous, congé entre bords, limiter, diviser…
